嵟廔峏怴擔: 2003擭11寧8擔乮搚梛擔乯
TMO偱偼枅擭偺暥壔嵳偱偄傜偟偨曽偵慖傝偡偖偭偨栤戣傪偍弌偟偟偰偄傑偡丅崱擭傕椙栤傪擄堈搙偝傑偞傑偵庢傝懙偊傑偟偨丅1栤偱傕夝偐傟偨傜偍嬤偔偺MATHIC夛堳偵偍抦傜偣偔偩偝偄丅偦偺応偱摉斲傪敾掕偄偨偟傑偡丅栤戣偼丄侾侽斣傪彍偄偰丄侾栤偵偮偒僩儔僀儅僗儘儞億僀儞僩侾侽揰偱偡丅儊乕儖偱摎埬傪偍憲傝偄偨偩偗傟偽丄嵦揰傪偟偰寢壥傪曉怣偟傑偡偺偱丄偦偪傜傕偛棙梡偔偩偝偄丅
亙栤亜捀妏偑偦傟偧傟俁侽亱丆侾俆侽亱偺擇偮偺擇摍曈嶰妏宍A偲B偑偁傝傑偡丅偙傟傜偼掙曈偑摍偟偔丄崅偝傪懌偡偲侾偵側傝傑偡丅偙傟傜偺嶰妏宍偺掙曈偺挿偝傪媮傔偰偔偩偝偄丅
恾偺傛偆偵A偲B傪掙曈偱偔偭偮偗傞偲懳妏慄偑屳偄偵悅捈側
亙摎亜巐妏宍乮扂宍乯偵側傝傑偡丅
偙偺巐妏宍偺塃敿暘傪愗偭偰丄嵍敿暘偵偔偭偮偗傞偲丄
俁侽亱丆俈俆亱丆俈俆亱偺2摍曈嶰妏宍偑弌棃傑偡丅偙傟偺柺愊偼侾亊侾乛俀丂亐俀亖1乛係丏偙傟偼扂宍偺柺愊偲摍偟偄偺偱丄掙曈偼1乛係亊俀亐侾亖侾乛俀丅
丂
摎丗侾乛俀
丂
丂
亙栤亜婯懃惈傪尒偮偗偰摎偊偰偔偩偝偄丅
俠俙俿亖侾俁俈侾丄俢俷俧亖俀俁俋俉丄俥俬俽俫亖俋俁俈俇俁偺偲偒丄俵俙俿俫亖丠
丂
亙摎亜偙傟偼丄A亖侽丆B亖侾丆C亖俀丆D=3丆丒丒丒丆X亖俀俆偲偄偆傛偆偵A乣X偵侽乣俀俆偺斣崋傪偮偗丄26恑朄偱撉傫偩傕偺偱偡丅乮傾儖僼傽儀僢僩偼俀俇暥帤乯
椺偊偽丄CD亖俀俁乮26恑朄乯亖俀亊俀俇亄俁亖俆俆偲側傝傑偡丅
傾儖僼傽儀僢僩偼丄ABCDEFGHIJKLMNOPQRSTUVWXYZ偲暲傫偱偄傞偺偱丄
M亖侾俀丆A亖侽丆T亖侾俋丆H亖俈側偺偱丄
MATH亖侾俀亊俀俇亊俀俇亊俀俇亄侽亊俀俇亊俀俇亄侾俋亊俀俇亄俈
亖俀侾侾係侾俁
丂
摎丗俀侾侾係侾俁
丂
亙栤亜師偺悢偺楍偺婯懃惈傪尒偮偗偰丄仩偵擖傞悢傪摉偰偰偔偩偝偄丅
俀丆係丆俉丆俈丆俆丆侾侽丆侾侾丆仩丆俉丆俈丆侾係丆丒丒丒
丂
亙摎亜俀丆係丆俉偲偔傟偽丄侾俇丆俁俀丆俇係丆丒丒丒偱偡偹丅
侾俇丆俁俀丆俇係傪俈丆俆丆侾侽偺壓側偳偵彂偄偨恖偼偙偺偁偨傝偱傕偆暘偐偭偨偱偟傚偆丅偦偆丄奺寘偺榓傪庢偭偨傕偺偵側偭偰偄傞偺偱偡丅
侾俀俉偵懳偟偰偼丄侾亄俀亄俉偱侾侾丆俀俆俇偵懳偟偰偼丄俀亄俆亄俇偱侾俁丏
傛偭偰仩偵擖傞偺偼侾俁偵側傝傑偡丅

亙栤亜恾偺傛偆側儅僗栚偵9屄偺堎側傞1埲忋偺惍悢傪擖傟偰丄廲墶幬傔偺偳偺楍偺3偮偺悢傪妡偗崌傢偣偰傕摍偟偄抣偵側傞傛偆偵偟傑偡丅偙偺偲偒丄偦偺乽摍偟偄抣乿偼嵟彫偱偄偔偮偱偟傚偆丅
亙摎亜摎偼俀侾俇偱偡丅偙傟傪徹柧偟傑偟傚偆丅傑偢丄
俁丂丂係丂丂侾俉
俁俇丂俇丂丂丂侾
俀丂丂俋丂丂侾俀
偺傛偆側傕偺偑偁傞偺偱丄俀侾俇枹枮偺傕偺偑側偄偙偲傪帵偟傑偟傚偆丅
偦傟偧傟偺悢偑慺悢倫偱壗夞妱傝愗傟傞偐傪峫偊傑偡丅乮偨偩偟丄俋偮偺悢偺偆偪偳傟偐偼倫偱妱傝愗傟傞偲偟傑偡乯
偙偺偲偒丄偦傟傜偼偨偰丆墶丆側側傔偺榓偑摍偟偔側傝傑偡丅
乮椺偊偽丄忋偺曽恮偱尵偆側傜偽丄倫亖俁偺偲偒
侾丂丂侽丂丂俀
俀丂丂侾丂丂侽
侽丂丂俀丂丂侾丂丂
偲側偭偰丄妋偐偵廲墶側側傔偺榓偑偡傋偰俁偵側偭偰偄傑偡丅乯
偦偺乽摍偟偄抣乿偑俁埲忋偱偁傞偙偲傪傑偢帵偟傑偡丅
傑偢丄侽偩偲偡傞偲慡偰侽偵側傝柕弬丅
侾偩偲偡傞偲丄侽偲侾偺傒傪偮偐偭偰嶌傜偹偽側傜側偄偑偦傟偼柧傜偐偵晄壜擻乮彮偟挷傋傟偽暘偐傝傑偡乯傑偨丄偁傞倫偵偮偄偰傒偨偲偒偺榓偺乽摍偟偄抣乿偑俀偩偭偨偲偡傞丅
偡傞偲偙傟偼侽偲侾偵傛偭偰偺傒嶌傜傟偰偄傞偙偲偑偡偖傢偐傞丅
偙傟傕嶌傟側偄偙偲偑柧傜偐側偺偱丄
丂
師偵丄忋偺傛偆側倫偺屄悢偑壗屄偱偁傞偐偵傛偭偰応崌暘偗偟傑偡丅
乮侾乯堦偮偺偲偒
偦偺偲偒丄倫傪俀偵偡傞偺偑柧傜偐偵嵟彫偱偡偑丄偙偺偲偒慡偰堎側傞悢偱側偗傟偽側傜側偄偲尵偆忦審偵傛傝丄乮侽亄侾亄俀亄丒丒丒亄俉乯乛俁亖侾俀側偺偱俀侾俀埲忋丅
乮俀乯俀偮偺偲偒
忋偱帵偟偨偙偲傛傝俀俁俁俁亖俀侾俇埲忋丅
乮俁乯俁偮埲忋偺偲偒丄
俀俁俁俁俆俁乮亜俀侾俇乯埲忋丅
丂
俀侾俀亜俀侾俇側偺偱帵偝傟偨丅
丂
摎丗俀侾俇
丂
亙栤亜2寘偺惍悢偵懳偟丄師偺傛偆側憖嶌傪偟傑偡丅
乮憖嶌乯偦偺悢傪暲傃懼偊偰嵟戝偵側傞傕偺亅嵟彫偵側傞傕偺
丂丂丂丂偵偦偺悢傪抲偒姺偊傞丅抲偒姺偊偨悢偑俀寘偱側偗傟偽丄偦偙偱憖嶌傪廔椆偡傞丅
幚偼丄偳偺2寘偺惍悢偵懳偟偰傕偄偮偐憖嶌偑廔傢傝傑偡丅偱偼丄嵟懡偱壗夞偐偐傞偱偟傚偆丅
丂
亙摎亜傑偢嵟弶偵偍榣傃偱偡丅暥壔嵳堦擔栚偺嵦揰偱丄杮摉偼俆偑惓夝偺偲偙傠傪係偑惓夝偲偟偰偄傑偟偨丅怽偟栿偁傝傑偣傫偱偟偨丅
丂
傑偢丄嵟戝偵側傞傕偺傪侾侽倎亄倐偲偍偔偲丄嵟彫偵側傞傕偺偼侾侽倐亄倎側偺偱丄
堦夞憖嶌傪偡傞偲丄俋乮倎亅倐乯偲側傝丄俋偺攞悢丅傛偭偰丄俋偺攞悢偺傒挷傋傟偽傛偄丅
侾俉仺俇俁仺俀俈仺係俆仺俋丂丂丂丂丂
偦傟埲奜偼偙傟傪搑拞偐傜偨偳傞偙偲偵側傞偺偱偙傟偑嵟懡乮係夞乯丅
傑偨丄俀係仺侾俉側偺偱幚嵺偵堦夞憖嶌傪偡傞偲侾俉偵側傞傕偺偑偁傞丅
傛偭偰係亄侾亖俆夞丅
丂
摎丗俆夞
丂
亙栤亜奺寘偺3忔傪偡傋偰懌偡偲尦偺悢偵側傞傛偆側1埲忋偺惍悢傪慡偰媮傔偰偔偩偝偄丅
丂丂丂丂乮A偺3忔偲偼丄A亊A亊A偺偙偲丅乯
丂
亙摎亜傂偨偡傜挷傋傑偟傚偆丅揔摉偵応崌暘偗偟偰抧摴偵傗傟偽慡偰尒偮偐傝傑偡丅
丂
摎丗侾丆侾俆俁丆俁俈侽丆俁俈侾丆係侽俈
丂
亙栤亜偁側偨偼俵俙俿俫俬俠偵戝廜徿傪搳昜偡傞丅Yes偐No偐丅
(嫀擭偺惓摎棪侾侽侽亾亖俵俙俿俫俬俠挷傋)
丂
亙摎亜摎傪尵偆昁梫偼側偄偱偟傚偆丅戝廜徿傪搳昜偟偰偔傟偨奆偝傫偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅
丂
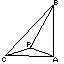
亙栤亜塃恾偱丄仮俙俛俠偼妏俙偑捈妏偺擇摍曈嶰妏宍丄佢俹俛俠亖15亱丄佢俹俠俛亖30亱偺偲偒丄佢俹俙俛傪媮傔偰偔偩偝偄丅
丂
亙摎亜揰俢傪捈慄俙俛偵懳偟俹偲摨偠懁偵俙俛俢偑惓嶰妏宍偵側傞傛偆偵偲傞丅
佢俙俛俢亖俇侽亱丂丂乗乗乗嘆
佢俛俙俢亖俇侽亱丂丂乗乗乗嘇
俙俛亖俙俢丂丂乗乗乗嘊
傑偨丄仮俙俛俠偑捈妏擇摍曈嶰妏宍側偺偱
佢俙俛俠亖係俆亱丂丂乗乗乗嘋
佢俙俠俛亖係俆亱丂丂乗乗乗嘍
佢俛俙俠亖俋侽亱丂丂乗乗乗嘐
俙俛亖俙俠丂丂乗乗乗嘑
嘆丆嘋傛傝佢俠俛俢亖侾俆亱丂丂乗乗乗嘒
嘊丆嘐傛傝俙俠亖俙俢丂丂乗乗乗嘓丂丂
嘇丆嘐傛傝佢俠俙俢亖俁侽亱丂丂乗乗乗嘔
嘓丆嘔傛傝佢俙俠俢亖俈俆亱丂丂乗乗乗嘕
嘍丆嘕傛傝佢俛俙俢亖俁侽亱丂丂乗乗乗嘖
嘒丆嘖傛傝丄仮俛俹俠偲仮俛俢俠偼崌摨丅
傛偭偰丄俛俢亖俛俹丏傑偨丄仮俙俛俢偑惓嶰妏宍側偺偱丄俛俢亖俙俛
傛偭偰丄俙俛亖俛俹丅
傑偨丄佢俙俛俹亖俁侽亱傛傝丄佢俛俙俹亖俈俆亱
丂
摎丗俈俆亱
丂
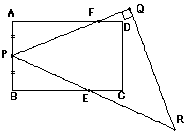
亙栤亜塃恾偱丄俙俛俠俢偼挿曽宍偱丄俹俻俼偼俻偑捈妏偺嶰妏宍偱丄俙俹亖俙俛丄俹俥亖俋丄俥俻亖俁丄俹俤亖係丄俤俼亖俋偱偡丅
偙偺偲偒丄榋妏宍俙俛俤俼俻俥偺柺愊傪媮傔側偝偄丅
丂
亙摎亜嶰妏宍俙俹俥傪俹傪拞怱偵夞揮偝偣偰丄俙偑俛偵廳側傞傛偆偵偡傞丅偙偺偲偒俥偑堏摦偟偨揰傪俧偲偡傞偲丄乮榋妏宍俙俛俤俼俻俥偺柺愊乯亖乮巐妏宍俧俤俼俻偺柺愊乯丂丂偲側傞丅
俹俻亖侾俀丆俹俼亖侾俁丆佢俹俻俼亖俋侽亱傛傝俻俼亖俆
乮嶰妏宍俹俻俼偺柺愊乯亖俹俻亊俻俼乛俀亖侾俀亊俆乛俀亖俁侽
乮嶰妏宍俤俻俼偺柺愊乯亖乮嶰妏宍俹俻俼偺柺愊乯亊俤俼乛俹俼亖俁侽亊俋乛侾俁亖俀俈侽乛侾俁
乮嶰妏宍俤俹俻偺柺愊乯亖乮嶰妏宍俹俻俼偺柺愊乯亊俹俤乛俹俼亖俁侽亊係乛侾俁亖侾俀侽乛侾俁
乮嶰妏宍俧俤俻偺柺愊乯亖乮嶰妏宍俤俹俻偺柺愊乯亊俧俻乛俹俻亖侾俀侽乛侾俁丂亊俀侾乛侾俀亖俀侾侽乛侾俁
乮巐妏宍俧俤俹俻偺柺愊乯亖乮嶰妏宍俧俤俻偺柺愊乯亄乮嶰妏宍俤俻俼偺柺愊乯
亖俀俈侽乛侾俁亄俀侾侽乛侾俁亖係俉侽乛侾俁
丂
摎丗係俉侽乛侾俁
丂
亙栤亜堦曈侾偺棫曽懱傪丄柺愊俽偺惓曽宍偱曪傓丅
偙偺偲偒俽傪側傞傋偔彫偝偔偟偰偔偩偝偄丅
丂
亙摎亜柺愊偑敧偺惓曽宍偺惓曽宍偱丄恾偺巼偺晹暘傪巊偭偰暍偆傛偆偵偡傟偽曪傔傑偡 乮偪傚偆偳忋偺柺偵巐曽岦偐傜捈妏擇摍曈嶰妏宍偑忔傞丅傢偐傝偵偔偔偰偡傒傑偣傫丅曪傓傾僯儊乕僔儑儞偲偐嶌傟側偄偺偱偙傟偱姩曎娋乯

堦墳俉偑嵟彫偱偁傞偙偲偺徹柧偼弌棃偨偺偱偡偑丄
偙偙偱偼擄偟偄偺偱徯夘偼偟傑偣傫丅
丂