最終更新日: 2001年2月18日(日曜日)
JMO(日本数学オリンピック)は国際数学オリンピックの予選も兼ねた大会で、高校生まで参加できる。われわれMATHICからは今回は9名中学生が参加した。
解説の記述の中に数学に関する知識を前提としたものがある。ごまかしているような気がして後ろめたい。これらについては説明のページを「数学小技集」や「数学用語の森」の中にもうけてリンクを張るつもりである。お待ち下さい。ただ、管理者にメールで訊いて下さればお答えするし、質問を受けたところを優先してページ上で説明していく。
このページの問題は、(財)数学オリンピック財団の「2001年第11回日本数学オリンピック予選問題」からの引用です。問題部分の著作権は(財)数学オリンピック財団に帰属します。もちろん解答と解説はMATHICの手になるものです。
2001をある正の整数nで割ったところ、余りは114になった。このようなnのうち、最小のものを求めよ。ただし、n>114である。
2001をnで割った余りが114ということは、
2001 = kn + 114 (kは正の整数).
kn = 2001 - 114
kn = 1887.
つまり、nは1887の約数である。1887の114より大きい約数のうち最小のを求めればよい。1887 = 3×17×37なので、1887の約数は1, 3, 17, 37, 51, 111, 629, 1887の8つである。114より大きいのは629と1887であるが、このうち小さいのは629(解答)である。
縦の長さが8、横の長さが7の長方形の中に、5つの合同な正方形が下図のように詰め込まれている。正方形の一辺の長さを求めよ。
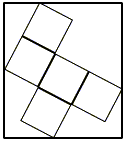
正方形の1辺に着目する。正方形の1辺の両端からそれぞれ長方形の縦の辺、横の辺に平行な直線を引くと、直角三角形ができる。この直角三角形の斜辺が求める長さである。斜辺をのぞいた2辺のうち、短い方の長さをa、長い方の長さをbとして図に書き込んでいく。縦の長さと横の長さをみることで次の2式が得られる。
a + 3b = 7,
2a + 3b = 8.
連立方程式として解くと、
a = 1, b = 2.
先の直角三角形で、求める長さ(斜辺)をcとおき三平方の定理を使うと、
a2 + b2 =c2.
先に求まったaとbの値を代入すると、
c2 = 5
c = (√5)(解答)
2001個の自然数1,2,3, ... ,2001の中から何個かの数を一度に選ぶとき、選んだ下図の総和が奇数であるような選び方は何通りあるか。
ただし、1個も選ばないときはその総和は0であると約束する。また、2001個すべてを選んでもよい。
1から2001の数は偶数と奇数からなる。だから偶数をどう選ぶかと奇数をどう選ぶかを別々に決めると1から2001までの数から何を選ぶのか決まるはずだ。
まず偶数の選び方を考える。偶数をどう選んでも足し合わせると偶数になる。総和が偶数か奇数かには全く関係しない。だから偶数は自由に選んで良い。1から2001には1000個の偶数が入っている。そのそれぞれについて選ぶか選ばないかの二者択一をしていくのだから、偶数の選び方は21000通り。
また、偶数はいくつ足しても偶数なのだから、奇数の総和は奇数になればよいことが分かる。いくつかの奇数の総和が奇数であるということは、奇数個の奇数を足し合わせたということである。1から2001まで1001個ある奇数の中から奇数個選ぶのに何通りあるのかが分かればよい。
さて、たくさんあるものの中から奇数個選ぶのに何通りあるのかどうやって数えたらいいのか考える。最後の一つを除いて自由に選べば最後が決まって丸くおさまることが分かる。つまり、最後からふたつ目まで選ぶか選ばないか決まった段階で、それまでに偶数個選んでいれば最後の一つは選ぶし、それまでに奇数個選んでいたのなら最後の一つは選ばなけらばよい。
ということで、1001個の奇数の中から奇数個の奇数を選ぶことは、そのうちの1000個について選ぶか選ばないかの二者択一を自由にすることと同じだと分かった。このやり方は21000通り。
偶数の選び方と奇数の選び方とは無関係に定めて問題ないから、1から2001までの数の可能な選び方の総数は、21000 × 21000 = 22000通り(解答)
一辺の長さaの正三角形ABCがある。D,E,Fはそれぞれ辺BC,CA,AB上の点であり、三角形DEFは一辺の長さbの正三角形である(ただしb<a)。このとき、三角形AFEの内接円の半径の長さを求めよ。
図は作成中...今のところはお描き下さい。
まず三角形AFBの面積をa,bで表してみる。
3△AFB = △ABC - △DEF = (ルート3)(a2 - b2) / 4
△AFB = △ABC - △DEF = (ルート3)(a2 - b2) / 12
三角形の内接円の半径は面積の2倍を外周の長さで割ったものに等しい(説明要りますね...)から、△AFBの内接円の半径をrとすると、
r = 2△AFB / (FE + EA + AF) = 2△AFB / (a + b)
先にa,bで表した△AFBの面積を代入すると、
r = (ルート3)(a2 - b2) / 6(a + b) = {(ルート3)/6}(a - b)(解答)
12001 +2 2001 + 32001 + ・・・ + 20002001 + 20012001を13で割ったときの余りを求めよ。
まず合同式についての解説を読んでいただきたい。
以後の合同式は、mod.13のもとでのものである。まず、合同式では成り立っている式同士の両辺それぞれを掛け合わせても成り立つことから、両辺の累乗を取って、
n ≡ n + 13
∴n2001 ≡ (n + 13)2001.
この式はどんなことを表しているのか具体的な例を挙げると、
12001 ≡ 142001 ≡ 272001...
12001 + ... + 132001 ≡ 142001 + ... + 262001
つまり、仮に12001 + 22001 + ... + 122001 + 132001 ≡ kとすると、2001 = 13×154 - 1より、
12001 +2 2001 + 32001 + ・・・ + 20002001 + 20012001
≡ 154k - 20022001 ≡ 154k - 02001 ≡ 154k.
なのでkを求めれば答えが求まる。ところが、脈絡なく選んだ整数aについて次の式が成り立つ。
a2001 + (-a)2001 = 0
a2001 + (-a)2001 ≡ 0
a2001 + (13 - a)2001 ≡ 0.
つまり、
02001 + 132001 ≡ 0
12001 + 122001 ≡ 0
22001 + 112001 ≡ 0
32001 + 102001 ≡ 0
42001 + 92001 ≡ 0
52001 + 82001 ≡ 0
62001 + 72001 ≡ 0
合計して、
k ≡ 0.
答えは、
154k ≡ 0(解答)
座標平面上に、原点O(0,0)、点A(1,0)がある。点Pは半直線x=0,y≧1上を、点Qは半直線x=1,y≧1上を、四角形OAQPの面積が常に2となるように動く。点B(¼,0)と直線PQの距離がとりうる最大の値を求めよ。
ただし、点Bと直線PQの距離とは、点Bから直線PQにおろした垂線の長さのことである。
Pの座標を(0,p)と書き、Qの座標を(0,q)と書くことにする(p≧1,q≧1)。
四角形OAQPは、OP//AQだから台形である。面積を考えると、
(台形OAQP) = (OP + QA)×OA/2
(台形OAQP) = (p + q)/2.
問題の条件(台形OAQP) = 2を代入すると、
p + q = 4.
さて、PQの中点Mの座標を求めると、
M = ((0 + 1)/2, (p + q)/2)
M = (1/2, 2).
もちろんPQは常にMを通る。P、Qの動きにつれて変化するのは傾きである。Bからの距離を最大にすればよい。
PQとBの距離はBM以上にはならない。PQとBとの距離はPQ上の点の中でもっともBに近い点とBとの間の距離だからである。
さらに、PQとBとの距離をBMにしたときに条件に反しないことを確かめればBMの値を最大距離として答にできる。PQとBとの距離をBMにするのは、PQ⊥BMにするということである。このときのPQの傾きを求めてみる。PQの傾きはq - pであるからこれを使い、BMの傾きはbということにする。
b = (2 - 0)/{(1/2) - (1/4)} = 8
PQ⊥BMなので、
(q - p)b = -1 (説明要りますね...)
これにbの値を代入すれば、
q - p = -1/8.
先に求めた和(p + q = 4)と合わせて計算すれば、
p = 33/16,
q = 31/16.
これは問題文にあった条件(p≧1,q≧1)をこれらはみたしている。
故に、答は、
BM = (√65)/4.(解答)
4×4のマス目をつくり、1から4までの数字をそれぞれ4つずつ書きこむ。ただし、以下の3つの条件をみたすとする。

このような図の書き込み方は何通りあるか。
まず、下図の青く塗ったところに数を入れれば残りにはいる数は全部決まることを説明する。(お待ち下さい、というかアイデアあったら教えて。)

次に、青く塗ったところに条件をみたすように数を入れたとき、残りの部分を埋めるときに矛盾が起きないことを説明する。(お待ちを、というかアイデアあったら下さい。)
以上より、図の書き込み方の数は青い部分の書き込み方の数と等しいことがわかった。
答は、右上部分の入れ方4!と左下部分の入れ方4×3を掛け合わせ、
4!×4×3 = 288通り(解答)
2つの方程式
x5 + 2x4 - x3 - 5x2 - 10x + 5 = 0
x6 + 4x5 + 3x4 - 6x3 - 20x2 - 15x + 5 = 0
を共にみたす実数xをすべて求めよ。
一番目の式の左辺で二番目の式の左辺を割る(説明要りますね...)ことによって次のことがわかる。
x6 + 4x5 + 3x4 - 6x3 - 20x2 - 15x + 5 = (x5 + 2x4 - x3 - 5x2 - 10x + 5)(x + 2) + (x3 - 5)
わかっている値を代入すると、
x3 - 5 = 0
よってx = 3√5(解答)
∠ABC = 2∠ACBとなる三角形ABCにおいて、∠BACの二等分線と辺BCとの交点をDとする。AB = CDのとき∠BACは何度(゚)か。ただし、線分XYの長さをXYで表す。
図は作成中なので、今のところはお描き下さい。
問題文に加え、角ABDの二等分線とADとの交点をEとする。
ここで記号を定める。
a = AB = CD
x = ∠BAD = ∠DAC
y = ∠ABE = ∠EBD = ∠ACD
b = BD
三角形ABDと三角形ACDについて、
∠ABE = ∠ACD (= y),
∠EAB = ∠DAC (= x).
よって、三角形ABDと三角形ACDは相似である。ゆえに、
AC = a×AD/AE.
ところで、BEは角ABDの二等分線なので、
AE:ED = AB:BD = a:b.
AD/AE = (a + b)/a.
先の式に代入して、
AC = a×(a + b)/a = a + b = BC.
ということは、三角形ABCは二等辺三角形である。二等辺三角形の底角は等しいから、
2x = ∠CAB = ∠ABC = 2y
x = y.
三角形ABCの内角の和は180度だから、
180゚ = ∠ABC + ∠BCA + ∠CAB = 5x
x = 36゚
答、∠CABは2xだから、
72゚(解答)
空間内に10個の異なる平面がある。どの2個の平面も一つの直線を共有し、どの3個の平面もただ1点のみを共有し、どの4個の平面も共有点を持たない。これら10個の平面によって空間はいくつの部分に分割されるか。
いきなり10個のことなる平面について考えるのではなく、一枚ずつ加えていってどのように空間が区切られるのかみていこう。ここでは、区切られた空間を「部屋」と呼ぶことにする。
まず、全く区切られていないとき、部屋は一つである。
次に、1枚の平面を空間の中に置くと空間は2つの部分に分けられる。部屋の数は1つ増えたわけだ。
2枚目の平面を加える。2枚目の平面は1枚目の平面と一直線を共有して、つまり交わっている。部屋数は4つになるのは当たり前のように思われる。しかしあとあとのために敢えてややこしく次のように考えておく。2枚目の平面は1枚目の平面によって2つの部分に区切られている。区切られたそれぞれの半平面が部屋数を1つずつ増やすのだから部屋数は2つ増えて4つになるのだと考える。
3枚目の平面を加える。3枚目の平面は1枚目とも2枚目とも交わるが、しかし3平面は1点のみを共有する。このとき、3枚目の平面は1枚目と2枚目によって4つの部分に分けられる。4つの部分それぞれが部屋数を1つずつ増やすから部屋数は4つ増えて8つになる。
ここまでは1, 2, 4, 8と部屋数は平面を加えるごとに倍になっている。
しかし、4枚目を加えたとき異変が起きる。4枚目の平面は、1,2,3枚目でいくつの部分に区切られるだろうか。これらの平面と4枚目は交わるのだから、4枚目で1,2,3枚目を斬ると切り口にそれぞれ直線としてあらわれる。3枚平面をとると1つ共有点があるはずだから、切り口の直線を2本とれば必ず交わっているはずである。4つの平面は共有点を持たないから、切り口の直線3本は1点で交わるのではない。言い換えると、三角形を囲んでいる。
つまり、4枚目の平面が1,2,3枚目によっていくつに分けられるかの答は、平面を3本の直線でいくつに分けられるかの答になっている。ただし、3本の直線はどの2つをとっても交わり、しかも3本が一つの点には集まっていないという条件が付く。答は7である。だから、4枚目の平面は部屋数を7増やし、部屋数は15になる。
あとは同様に10枚目まで加えていけばよい。n枚目を加えるときに部屋数は「n-1本の直線が平面を区切ってできる部分の数」だけ増えるのだ。紙の上に線を引けば求まる数である。しかしそれでは100枚の平面の場合に対応するのが大変ではないか。私は断固計算する。
というわけで、問題は平面を直線で仕切る問題に還元された。
では、「n-1本の直線が平面を区切ってできる部分の数」はどうやって求めればいいのか。ここでも条件ができる。4枚目を加えたときの議論と同じように考えると、どの2本の直線をとってきてもどこかで交わっていて、どの3本の直線をとってきても1点には集まっていない。というものである。
これを数えるのも平面に1本ずつ直線を付け加えて行うことにしよう。
平面は1つの部分からなる。
ここに1本直線を通すと2つの部分に分かれる。部分の数は1増えた。
2本目の直線を通す。これは1本目と交わるはずである。だからこの直線は2本の半直線に分けられる。それぞれの半直線は部分の数を1ずつ増やすから、部分の数は2増えて4になる。
3本目の直線を通す。これは1本目とも2本目とも交わる。しかも3本は同じ点には集まらない。だから3本目は1,2本目によって、あわせて3本の線分、半直線に分けられる。それぞれが1ずつ部分の数を増やすから、部分の数は3増えて7になる。
空間を平面できる場合と違い、そろそろけりが付けられそうである。
n本目の直線を付け加えるときのことを考える。それまでに引かれたn-1本の直線おのおのと別の点で交わるので、n本目はnの部分に分けられる。だから部分の数はn増える。
これをもとにして計算すれば、10枚の平面で空間を区切ったときの部屋数は、
176個(解答)
正の整数nに対して、nの正の約数の総和をS(n)で表す。このとき、S(6n)≧12S(n)をみたす3桁の正の整数nは何個あるか。
S(n)を数式で表してみよう。nを2と3で割れるだけ割って素因数分解を途中まで進めた段階を考えると、nは下の式で表されるはずである。
n = 2a×3b×n' (a,bは0以上の整数, nは2とも3とも互いに素).
n'の約数がd1,d2, ... ,dmで総和がdだとしておく。そうすると、nの約数はどれも数式でしたのように表されるはずだ。
2t×3u×dv (0≦t≦a, 0≦u≦b, 0≦v≦m).
しかも上の式に代入するt,u,vを決めるとあらわれるnの約数も決まるはずなので、分配法則を用いると約数の総和は、
S(n) = (20 + 21 + ... + 2a)(30 + 31 + ... +3b)(d1 + d2 + ... dm)
等比数列の和についての知見を応用すれば、
S(n) = (2a+1 -1){(3b+1-1)/2}d
S(n)を数式で表すことができた。次はS(6n)を数式で表してみよう。最初の素因数分解が成り立っているとき、6nは下のように素因数分解される。
n = 2a+1×3b+1×n'
この式の中のa,b,n'が最初の式で使われた文字と同一であること注意しよう。さっき考えたことから、
S(6n) = (2a+2 -1){(3b+2-1)/2}d
問題は、S(6n)≧12S(n)をみたす数というのがどんな数なのか知ることにあるから、この不等式にさっき求まったa,b,dの式を代入してみよう。すると、
(2a+2 -1){(3b+2-1)/2}d ≧ 12(2a+1 -1){(3b+1-1)/2}d
dは正の整数であったから、dで式の両辺を割ることができる。ついでに2を掛ける。
(2a+2 -1)(3b+2-1) ≧ 12(2a+1-1)(3b+1-1)
(この間の説明は今考えています。何かアイデアがあったら教えて下さい。)
a,bは0以上の整数であるが、この中でこの不等式をみたすのはa = b = 0だけである。つまり、上の不等式を満たすnは6と互いに素である。
3桁の整数で6と互いに素なものの個数は、300個(解答)
5×9のマス目がある。次の条件をみたすように、各マスに1つずつ、0以上の実数を書き込む。
このような書き込み方が存在するような実数Sの最小値を求めよ。
2×3の枠を8枚使うと、重なりは生じるものの5×9のマス目を埋め尽くすことができる。だから、
S≧1/8.
ここでS=1/8となる並べ方があればいいのだが、それは以下の並べ方である。
| 1/8 | 0 | 0 | 0 | 1/8 | 0 | 0 | 0 | 1/8 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1/8 | 0 | 0 | 0 | 1/8 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/8 | 0 | 0 | 0 | 1/8 | 0 | 0 | 0 | 1/8 |
よって答は、1/8(解答)
以上